Sponsor Area
Differential Equations
Question
The volume of spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of balloon after t seconds.
Solution
Let v be volume of spherical balloon of radius r.
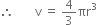...(1)
From given condition,
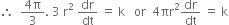
Separating the variables and integrating, we get.
...(2)
Now t = 0 when r = 3
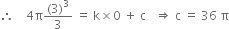...(3)
Again t = 3 when r = 6
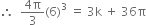
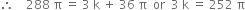
Putting
...(1)From given condition,
Separating the variables and integrating, we get.
...(2)Now t = 0 when r = 3
...(3)Again t = 3 when r = 6
Putting
Some More Questions From Differential Equations Chapter
Sponsor Area
Mock Test Series
Mock Test Series