Question
Find the particular solution of the differential equation 
given that y = 1, when x = 0.
Solution
The given differential equation is
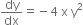
Separating the variables, we get,
Integrating,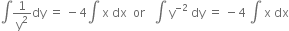
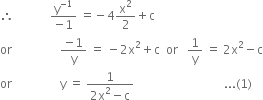
Now y = 1 when x = 0
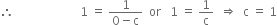
Putting c = -1 in (1), we get,
Separating the variables, we get,
Integrating,
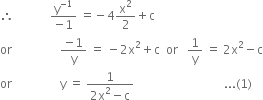
Now y = 1 when x = 0
Putting c = -1 in (1), we get,
