If z = x – i y and z^1/3 = p+ iq , then 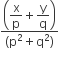$fraction numerator begin display style open parentheses straight x over straight p plus straight y over straight q close parentheses end style over denominator left parenthesis straight p squared plus straight q squared right parenthesis end fraction$ is equal to

1

-2

2

-1

Solution

-2

-1

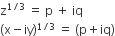straight z to the power of 1 divided by 3 end exponent space equals space straight p space plus space iq left parenthesis straight x minus iy right parenthesis to the power of 1 divided by 3 end exponent space equals space left parenthesis straight p plus iq right parenthesis

therefore,(Qz = x − iy)
(x - iy) = (p + iq)³
⇒ (x - iy) = p³ +(iq)³ + 3p²qi + 3pq²i²
⇒ (x - iy) = p³ - iq³ + 3p²qi - 3pq²
⇒ (x - iy) = (p³ - 3pq² ) + i (3p² q - q³ ) On comparing both sides, we get
⇒ x = (p³ - 3pq²) and - y = 3p² q - q³
⇒ x = p(p² - 3q² ) and y = q(q² - 3p² )

Some More Questions From Complex Numbers and Quadratic Equations Chapter

If the cube roots of unity are 1, ω, ω² then the roots of the equation (x – 1)³+ 8 = 0, are

The value of α for which the sum of the squares of the roots of the equation x² – (a – 2)x – a – 1 = 0 assume the least value is

If roots of the equation x² – bx + c = 0 be two consectutive integers, then b² – 4c equals

If z₁ and z₂ are two non-zero complex numbers such that |z₁ + z₂| = |z₁| + |z2| then argz₁ – argz₂ is equal to

If the equation a_nxⁿ +a_n-1x^n-1 +....... +a₁x =0, a₁ ≠ 0, n≥2, has a positive root x = α, then the equation na_nx^n-1 + (n-1)a_n-1x_n-2 +......+a₁ = 0 has a positive root, which is

For Daily Free Study Material Join wiredfaculty

Complex Numbers And Quadratic Equations

Some More Questions From Complex Numbers and Quadratic Equations Chapter

If the cube roots of unity are 1, ω, ω² then the roots of the equation (x – 1)³+ 8 = 0, are

The value of α for which the sum of the squares of the roots of the equation x² – (a – 2)x – a – 1 = 0 assume the least value is

If roots of the equation x² – bx + c = 0 be two consectutive integers, then b² – 4c equals

If z₁ and z₂ are two non-zero complex numbers such that |z₁ + z₂| = |z₁| + |z2| then argz₁ – argz₂ is equal to

If the equation a_nxⁿ +a_n-1x^n-1 +....... +a₁x =0, a₁ ≠ 0, n≥2, has a positive root x = α, then the equation na_nx^n-1 + (n-1)a_n-1x_n-2 +......+a₁ = 0 has a positive root, which is

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

Complex Numbers And Quadratic Equations

If z = x – i y and z1/3 = p+ iq , then is equal to 1 -2 2 -1

Some More Questions From Complex Numbers and Quadratic Equations Chapter

If the cube roots of unity are 1, ω, ω2 then the roots of the equation (x – 1)3 + 8 = 0, are

The value of α for which the sum of the squares of the roots of the equation x2 – (a – 2)x – a – 1 = 0 assume the least value is

If roots of the equation x2 – bx + c = 0 be two consectutive integers, then b2 – 4c equals

If z1 and z2 are two non-zero complex numbers such that |z1 + z2| = |z1| + |z2| then argz1 – argz2 is equal to

If the equation anxn +an-1xn-1 +....... +a1x =0, a1 ≠ 0, n≥2, has a positive root x = α, then the equation nanxn-1 + (n-1)an-1xn-2 +......+a1 = 0 has a positive root, which is

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

If the cube roots of unity are 1, ω, ω² then the roots of the equation (x – 1)³+ 8 = 0, are

The value of α for which the sum of the squares of the roots of the equation x² – (a – 2)x – a – 1 = 0 assume the least value is

If roots of the equation x² – bx + c = 0 be two consectutive integers, then b² – 4c equals

If z₁ and z₂ are two non-zero complex numbers such that |z₁ + z₂| = |z₁| + |z2| then argz₁ – argz₂ is equal to

If the equation a_nxⁿ +a_n-1x^n-1 +....... +a₁x =0, a₁ ≠ 0, n≥2, has a positive root x = α, then the equation na_nx^n-1 + (n-1)a_n-1x_n-2 +......+a₁ = 0 has a positive root, which is