Sponsor Area
Principle Of Mathematical Induction
Question
Statement − 1: For every natural number n ≥ 2 
Statement −2: For every natural number n ≥ 2,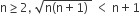
-
Statement −1 is false, Statement −2 is true
-
Statement −1 is true, Statement −2 is true, Statement −2 is a correct explanation for Statement −1
-
Statement −1 is true, Statement −2 is true; Statement −2 is not a correct explanation for Statement −1.
-
Statement − 1 is true, Statement − 2 is false.
Solution
C.
Statement −1 is true, Statement −2 is true; Statement −2 is not a correct explanation for Statement −1.
Hence Statement −2 is not a correct explanation of Statement −1.
Some More Questions From Principle of Mathematical Induction Chapter
Sponsor Area
Mock Test Series
Mock Test Series