Question
The conjugate of a complex number is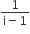 
. Then the complex number is
Solution
C.
The conjugate of a complex number is . Then the complex number is
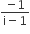
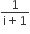
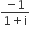
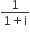
C.
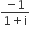
If the roots of the equation bx2+ cx + a = 0 be imaginary, then for all real values of x, the expression 3b2x2 + 6bcx + 2c2 is
The quadratic equations x2 – 6x + a = 0 and x2 – cx + 6 = 0 have one root in common. The other roots of the first and second equations are integers in the ratio 4 : 3. Then the common root is
All the values of m for which both roots of the equations x2 − 2mx + m2 − 1 = 0 are greater than −2 but less than 4, lie in the interval
If the cube roots of unity are 1, ω, ω2 then the roots of the equation (x – 1)3 + 8 = 0, are
The value of α for which the sum of the squares of the roots of the equation x2 – (a – 2)x – a – 1 = 0 assume the least value is
Mock Test Series
