The number of common tangent to the circles x²+y²-4x-6y-12=0 and x²+y²+6x+18y+26 = 0 is

• 1

• 2

• 3

• 4

C.

3

Number of common tangents depend on the position of the circle with respect to the each other.
(i) If circles touch externally ⇒C₁C₂  = r₁+ r₂,3 common tangents
(ii) If circles touch internally ⇒ C₁C₂ = r₂-r₁, 1 common tangents
(iii) If circles do not touch each other, 4 common tangents
Given  equations of circles are
x₂ +y²-4x-6y-12 = 0 .. (i) 
x²+y²+6x+18y+26 =0 ... (ii)
Centre of circle (i) is C1 (2,3) and radius
=
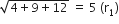
Centre of circle (ii) is C2(-3,-9) and radius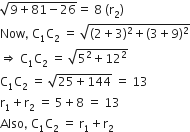

Thus, both circles touch each other externally. Hence, there are three common tangents.