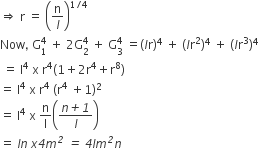Question
If m is the AMN of two distinct real numbers l and n (l,n>1) and G1, G2, and G3 are three geometric means between l and n, then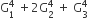 
equals
-
4l2 mn
-
4lm2n
-
4 lmn2
-
4l2m2n2
Solution
B.
4lm2n
Given,
m is the AM of l and n
l +n = 2m
and G1, G2, G3, n are in GP
Let r be the common ratio of this GP
G1 = lr
G2 =lr2
G3= lr3
n = lr4
