Sponsor Area
Relations And Functions
Convert each of the complex numbers given in the Polar form.
Here, z = 
Let z = 
...(1)
...(ii)
and 
...(iii)
Squaring and adding (ii) and (iii), we get
r2 = 4 
r = 2
From (ii), 
From (iii), 
since both 
are positive
∴ 
lies in 1st quadrant
∴ 
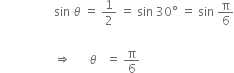
Putting in (i), we get
Which is the required polar form.
Hence,
Some More Questions From Relations and Functions Chapter
Fill in the blanks in the following table:
Numbers
Closed under
Addition
Subtraction
Multiplication
Division
Rational numbers
Yes
Yes
No
Integers
Yes
No
Whole numbers
...
Yes
Natural numbers
No
Numbers
Closed under
Addition
Subtraction
Multiplication
Division
Rational numbers
Yes
Yes
No
Integers
Yes
No
Whole numbers
...
Yes
Natural numbers
No
i9 + i19
3(7 + i7) + i(7 + i7)
Express each of the complex number given in the form of a + ib.
(1 - i) - (-1 + i6)
(1 - i) - (-1 + i6)
Express each of the complex number given in the form of a + ib.
(1 - i)4
(1 - i)4
Sponsor Area
Mock Test Series
Mock Test Series