Let S be the sum, P the product and R the sum of the reciprocals of n terms in a G.P. Prove that

Let a be the first term and r be the common ratio of a G.P.
                           S = the sum of n terms of G.P. = a + ar + .........ar^n-1

∴                                                                                            ...(i)
                           P = the product of n terms of G.P. = a. ar. ar²  .......  ar^n-1

∴                          P =
                                                                                          ...(ii)
      R = the sum of the reciprocals of n terms of G.P. =
          =
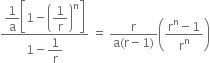
Now,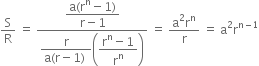         
L.H.S.    =
R.H.S. =

∴     L.H.S. = R.H.S.
Hence,