Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.

                                   OR

A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD = AD + BC.

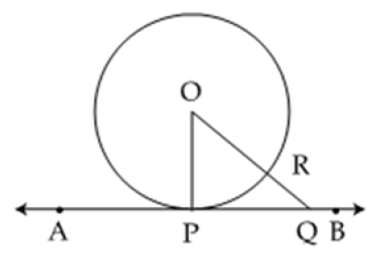
Given: AB is tangent to a circle with centre O.

To prove: OP is perpendicular to AB.

Constructions: Take a point Q on AB and join OQ.

Proof: Since Q is a point on the tangent AB, other than the point of contact P, so Q will be outside the circle.

Let OQ intersect the circle at R.

Now OQ = OR + RQ

$$\begin{gathered} \Rightarrow \mathrm{OQ}> \mathrm{OR} \Rightarrow \mathrm{OQ} > \mathrm{OP} .......[\mathrm{as} \mathrm{OR} = \mathrm{OP}] \\ \Rightarrow \mathrm{OP} < \mathrm{OQ} \end{gathered}$$

Thus OP is shorter than any other segment among all and the shortest length is the perpendicular from O on AB.

$\therefore \mathrm{OP} \perp \mathrm{AB}.$ Hence proved.

                                             OR

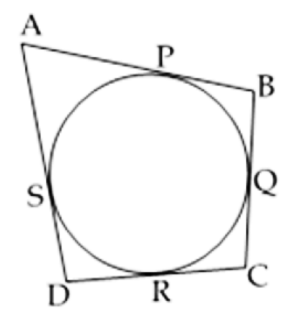
Let ABCD be a quadrilateral, circumscribing a circle.

Since the tangents drawn to the circle from an external point are equal,

we have,   

AP = AS       ..........(1)

BP = BQ       ..........(2)

RC = QC       ..........(3)

DR = DS       ..........(4)

Adding, (1), (2), (3) and (4), we get

AP + PB + RC + DR = AS + BQ + QC + DS

(AP + PB ) + (RC + DR ) = (AS + DS ) + (BQ + QC)

AB + CD = AD + BC.