Prove that the parallelogram circumscribing a circle is a rhombus.

                                       OR

Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Let ABCD be a parallelogram such that its sides touching a circle with centre O.

We know that the tangents to a circle from an exterior point are equal in length.

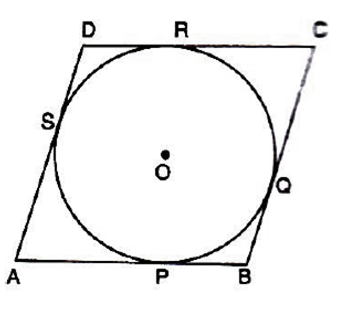
$\therefore$ AP = AS      .......[Tangnts  from point A]    .......(i)

    BP = BQ      .......[Tangents from point B]   .......(ii)

    CR = CQ      .......[Tangents from point C]   .......(iii)

and, DR = DS   .......[Tangents from point D]  ........(iv)

Adding (i), (ii), (iii), and (iv), we get

AP + BP + CR + DR = AS + BQ + CQ + DS

$\Rightarrow$(AP + BP) + (CR + DR) = ( AS + DS) + (BQ + CQ)

$\Rightarrow$AB + CD = AD + BC

$\Rightarrow$ 2AB = 2BC         [$\because$ ABCD is a parallelogram $\therefore$ AB = CD and BC = AD]

$\Rightarrow$AB = BC

Thus, AB = BC = CD = AD

Hence, ABCD is a rhombus.

                                         OR

A circle with centre O touches the sides  AB, BC, CD and DA  of a quadrilateral

ABCD at the points  P, Q, R and R respectively.

To prove:  $\angle \mathrm{AOB} + \angle \mathrm{COD} = 180° \mathrm{and}, \angle \mathrm{AOD} + \angle \mathrm{BOC} = 180°$

 Construction: Join OP, OQ, OR and OS.

Proof: Since the two tangents drawn from a external point to a circle

subtend equal angles at the centre.

$$\begin{gathered} \therefore \angle 1 = \angle 2, \angle 3 = \angle 4, \angle 5 = \angle 6 \mathrm{and} \angle 7 = \angle 8 \\ \mathrm{Now}, \angle 1 + \angle 2 + \angle 3 + \angle 4 + \angle 5 + \angle 6 + \angle 7 + \angle 8 = 360° \\ [\mathrm{Sum} \mathrm{of} \mathrm{all} \mathrm{the} \mathrm{angles} \mathrm{subtended} \mathrm{at} \mathrm{a} \mathrm{point} \mathrm{is} 360°] \\ \Rightarrow 2 ( \angle 2 + \angle 3 + \angle 6 + \angle 7) = 360° \mathrm{and} 2 (\angle 1 + \angle 4 + \angle 5 + \angle 8) = 360° \\ \Rightarrow ( \angle 2 + \angle 3 ) + (\angle 6 + \angle 7) = 180° \mathrm{and} (\angle 1 +\angle 8) +( \angle 4 + \angle 5) = 180° \\ \left[\therefore \angle 2 + \angle 3 =\angle \mathrm{AOB}, \angle 6 + \angle 7 = \angle \mathrm{COD} \angle 1 +\angle 8 =\angle \mathrm{AOD} \mathrm{and} \angle 4 + \angle 5 =\angle \mathrm{BOC}\right] \\ \Rightarrow \angle \mathrm{AOB} + \angle \mathrm{COD} = 180° \\ \mathrm{and} \angle \mathrm{AOD} + \angle \mathrm{BOC} = 180° \end{gathered}$$

Hence proved.