Tangents PA and PB are drawn from an external point P to two concentric circle with centre O and radii 8 cm and 5 cm respectively, as shown in Fig., If AP = 15 cm, then find the length of BP.

Solution

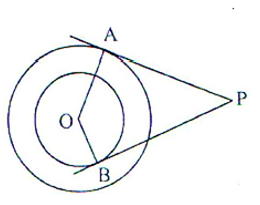
Given: Tangents PA and PB are drwan from an external point P to two

concentric circles with centre O and radii OA = 8 cm, OB = 5 cm

respectively. Also, AP = 15 cm.

Construction: We join the points O and P.

Proof: OA $⊥$ AP ; OB $⊥$ BP

[ Using the property that radius is perpendicular to the tangent at the

point of contact of a circle.]

In right angled triangle OAP,

OP² = OA² + AP² [ Using pythagoras theorem ]

= (8)² + ( 15 )² = 64 + 225 = 289

$∴$ OP = 17 cm

In right angled triangled OBP,

OP² = OB² + BP²

$\Rightarrow$ BP² = OP² - OB²

$\Rightarrow$ (17)² - (5)²

$\Rightarrow$ 289 - 25

= 264

$∴$ BP = $\sqrt{265}$ = 2 $\sqrt{66}$ cm.

For Daily Free Study Material Join wiredfaculty