Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.

Solution

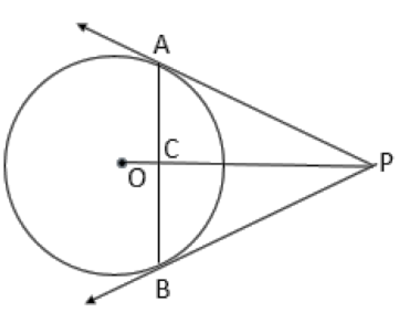
Let AB be a chord of circle with centre O.

Let AP and BP be two tangents at A and B respectively.

Suppose the tangents meet at point P. Join OP.

Suppose OP meets AB at C.

$Now in, ∆ PCA and ∆ PCB, PA = PB . . . . . . . . . . . . . (Tangents from an external point are equal) ∠ APC = ∠ BPC . . . . . . . . (PA and PB are equally inclined to OP) PC = PC . . . . . . . . . . (common) Hence, ∆ PAC ≅ ∆ PBC . . . . . . (by SAS congruence criterion) \Rightarrow ∠ PAC = ∠ PBC$

For Daily Free Study Material Join wiredfaculty

Circles

Prove that the tangents drawn at the end points of a chord of a circle make equal angles with the chord.

Some More Questions From Circles Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction