Question
A circle touches all the four sides of a quadrilateral ABCD. Prove that
AB + CD = BC + DA
Solution
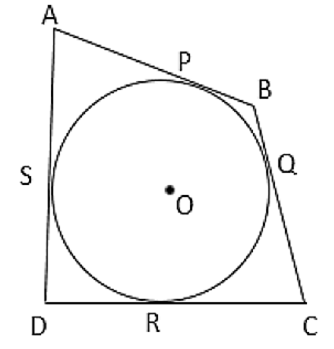
Since tangents drawn from an external point to a circle are equal in length, we have
AP = AS ........(i)
BP = BQ ........(ii)
CR = CQ ........(iii)
DR = DS ........(iv)
Adding (i), (ii), (iii), (iv), we get
AP + BP + CR + DR = AS + BQ + CQ + DS
( AP + BP ) + ( CR + DR ) = ( AS + DS ) + ( BQ + CQ )



