+91-8076753736[email protected]
logo
logo
-->

Some Applications Of Trigonometry

Question
CBSEENMA10009770
Wired Faculty App

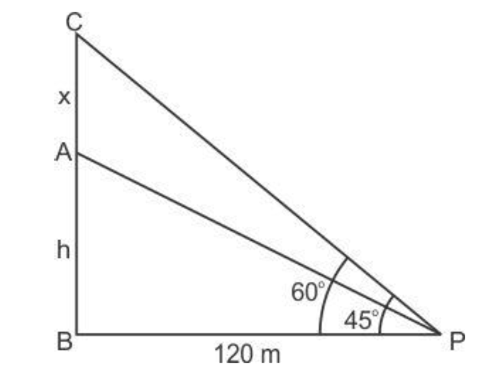
The angle of elevation of the top of a tower at a distance of 120 m from a point A on the ground is 45°. If the angle of elevation of the top of a flagstaff fixed at the top of the tower, at A is 60°, then find the height of the flagstaff. [Use 3 = 1.73 ]

Solution

Let AB is the tower of height h meter and AC is flagstaff of height x meter.

                         

 

∠APB = 45° and ∠BPC = 60°Tan60 = x + h120   3  =  x + h120 x + h = 1203          x =  1203 - h  Tan 45 = h120           1 = h120           h = 120Therefore height of the flagstaff = 1203 - 120                                                  = 120 ( 3 -1 ) m                                                  = 120 ( 1.73 - 1 ) m                                                  = 120 x 0.73 m                                                  = 87.6 m

Some More Questions From Some Applications of Trigonometry Chapter

In ΔABC, right angled at B. AB = 24 cm, BC = 7 cm. Determine:
(i) sin A cos A,
(ii) sin C, cos C.

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation