Prove that the tangent at any point of a circle is perpendicular to the radius through the point of contact.

Solution

Given: A circle C ( 0, r ) and a tangent l at point A.

To prove: OA $⊥$ l

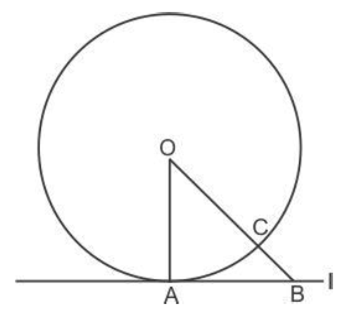
Construction: Take a point B, other than A, on the tangent l. Join OB. Suppose OB meets the circle in C.

Proof: We know that, among all line segment joining the point O to a point on l, the perpendicular is shortest to l.

OA = OC (Radius of the same circle)

Now, OB = OC + BC.

$∴ OB > OC \Rightarrow OB > OA \Rightarrow OA < OB (OC = OA = radius)$

But among all the line segments, joining the point O to a point on AB, the shortest one is the perpendicular from O on AB.

Hence OA is perpendicular to l.

For Daily Free Study Material Join wiredfaculty