Question
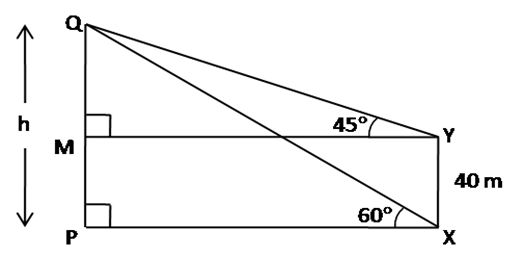
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60o. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of the tower is 45o. Find the height of the tower PQ and the distance PX. ![]()
Solution
Given the angle of elevation of the top Q of a vertical tower from the PQ from a point X on the ground is 60o.
From a point Y, 40 m vertically above X, the angle of elevation of the top Q of the tower is 45o.