Question
The ratio of the sums of the first m and first n terms of an A. P. is m2: n2. Show that the ratio of its mth and nth terms is (2m−1):(2n−1).
Solution
Let Sm and Sn be the sum of the first m and first n terms of the A.P. respectively. Let, a be the first terms and d be a common difference.
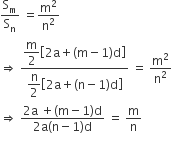
⇒[2a+(m−1)d]
n =[2a(n−1)d]m
⇒2an+mnd−nd=2am+mnd−md
⇒md−nd=2am−2an
⇒(m−n)d=2a(m−n)
⇒d=2a
Now, the ratio of its mth and nth terms is
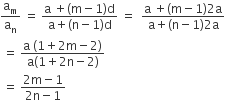
Thus, the ratio of its mth and nth terms is 2m – 1 : 2n – 1.
