Question
Two stations due south of a leaning tower which leans towards the north are at distances a and b from its foot. If, α, β, are the elevations of the top of the tower from these stations,
prove that its inclination ө to the horizontal is given by cot 
Solution
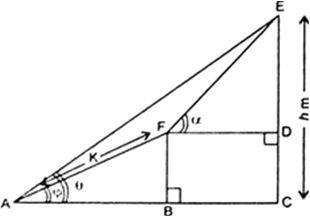
Let CE be the leaning tower. Let A and B be two given stations at distances a and b respectively from the foot of the tower.
Let CD = x and DE = h
In right triangle CDE, we have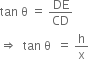
![]()
In right triangle BDE, we have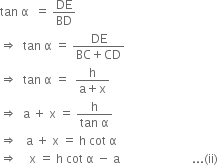
In right triangle ADE, we have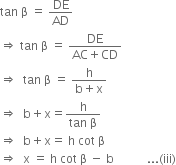
Comparing (i) and (ii), we get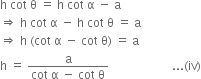
Comparing (i) and (iii), we get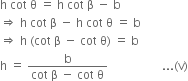
Comparing (iv) and (v), we get![]()

Hence, inclination ө to the horizontal is given by cot ![]()



