Question
A round balloon of radius r subtends an angle α at the eye of the observer while the angle of elevation of its centre is β. Prove that the height of the centre of the balloon is r sin β . cosec α/2.
Solution
Let P be the eye of observer. Let PA and PB are tangents to the round balloon.
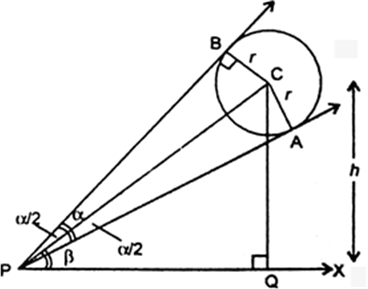
PX is the horizontal line and CQ ⊥ PQ. It is given that
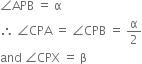
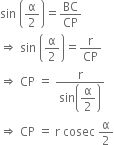
In right triangle CPQ, we have
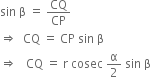
Hence, the height of the centre
= r sin

PX is the horizontal line and CQ ⊥ PQ. It is given that
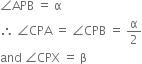
Let height of the centre C be h m and CA = CB = r
In right triangle CBP, we have
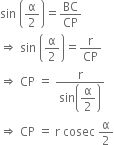
In right triangle CPQ, we have
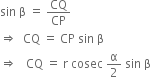
Hence, the height of the centre
= r sin



