Question
From a point 100 m above a lake, the angle of elevation of a stationary helicopter is 30° and the angle of depression of reflection of the helicopter in the lake is 60°. Find the height of the helicopter.
Solution
Let AB be the surface of the lake and P be the point of observation such that AP = 100 m. Let C be the position of the helicopter and C' be its reflection in the lake. Then,CB = C'B.
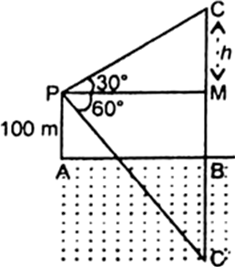
Let PM be perpendicular from P on CB. Then, ∠CPM = 30° and ∠CPM = 60°.
Let CM = h. Then, CB = h + 100 and CB = h + 100.
In right 
CMP,
In right 
PMC'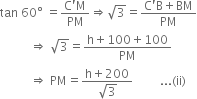
From (i) and (ii), we get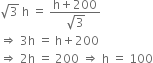
Now, CB = CM + MB = h + 100 = 100 + 100 = 200
Hence, the height of the helicopter from the surface of the lake = 200 m
