Question
The angles of depression of the top and the bottom of a 9 m high building from the top of a tower are 30° and 60° respectively. Find the height of the tower and the distance between the building and the tower.
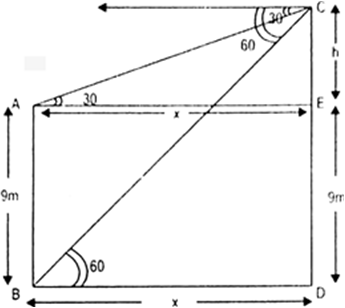
Solution
Let AB be the building such that AB = 9 m and CD is the tower. The angles of depression of the top and the bottom of the building from the tower are 30° and 60° respectively.
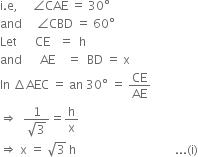
In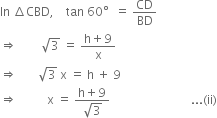
Comparing (i) and (ii), we get
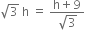
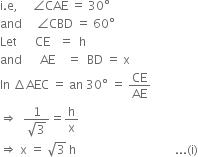
In
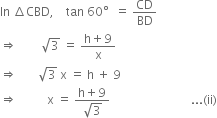
Comparing (i) and (ii), we get
⇒ 3h = h + 9
⇒ 3h - h = 9
⇒ 2h = 9
⇒ h = 4.5 m
Now, height of the tower
= (h + 9) met.
= (4.5 + 9) met.
= 13.5 met.
Difference between the building and tower (x)