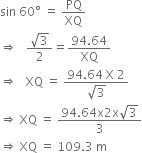Question
The angle of elevation of the top Q of a vertical tower PQ from a point X on the ground is 60°. At a point Y, 40 m vertically above X, the angle of elevation is 45°. Find the height of the tower PQ and the distance XQ.
Solution
Let PQ be the tower and Y is a point vertically above X such that XY = 40 m. The angle of elevation of the top Q from a point X on the ground is 60° and from a point Y vertically above the X be 45° i.e., ∠PXQ = 60° and ∠RYQ = 45°.
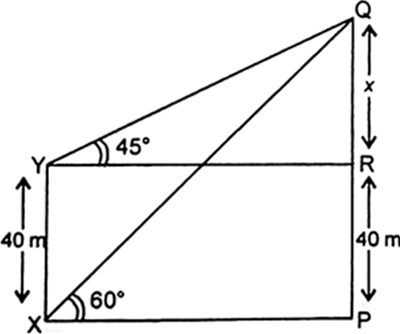

Let QR = x m
In right triangle QRY, we have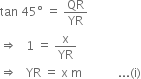
In right triangle QPX, we have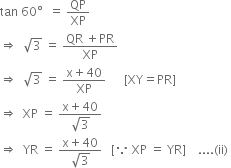
Comparing (i) and (ii), we get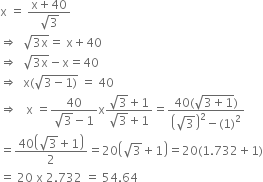
So, height of the tower PQ
= PR + QR
= 40 + x
= 40 + 54.64
= 94.64 m.
In right triangle QPX, we have