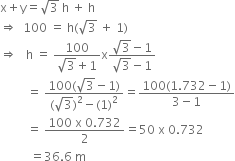Question
There is a small island in the middle of a 100 m wide river and a tall tree stands on the island. A and B are points directly opposite to each other on two banks and in line with the tree. If the angles of elevation of the top of the tree from P and Q are respectively 30° and 45°, find the length of the tree.
Solution
AQ = x m and BQ = y m and the angle of elevation of the top of the tree P from point A and B are 30° and 45° respectively.
i.e., ∠PAQ = 30° and ∠PBQ = 45°
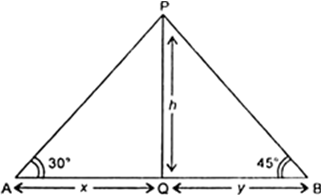
In right triangle
AQP, we have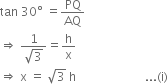
In right triangle BQP, we have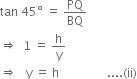
Adding (i) and (ii), we get