Question
From the top of a building 100 m high, the angles of depression of the top and bottom of a tower are observed to be 45° and 60° respectively. Find the height of the tower. Also find the distance between the foot of the building and bottom of the tower.
Solution
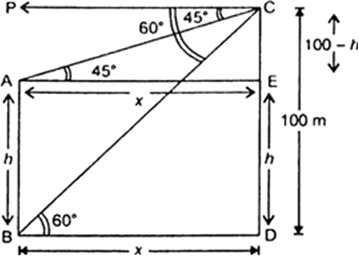
Let CD be the building such that CD = 100 m.
Let AB be the tower of height h metre. It is given that the angles of depression of the top A and the bottom B of the lower AB are 45° and 60° respectively.
i.e., ∠EAC = 45° and ∠DBC = 60°
Let BD = AE = x
In right triangle AEC, we have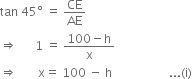
In right triangle BDC, we have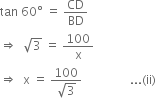
Comparing (i) and (ii), we get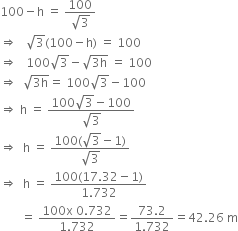
Hence,Height of tower (AB) = 42.26 m.



