+91-8076753736[email protected]
logo
logo
-->

Circles

Question
CBSEENMA10008342
Wired Faculty App

A boy standing on a horizontal plane finds a bird flying at a distance of 100 m from him at an elevation of 30°. A girl standing finds the angle of elevation of the same bird to be 45°. Both the boy and the girl are on opposite sides of the bird. Find the distance of bird from the girl.  

Solution

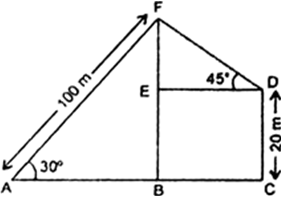
Let A be the position of boy D, be the position of girl and F be the position of kite, such that AF - 100 m; CD = 20 m; ∠BAF = 30° and ∠EDF = 45°
In right triangle ABF, we have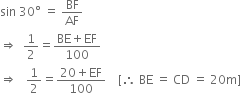
sin space 30 degree space equals space BF over AF rightwards double arrow space space 1 half equals fraction numerator BE plus EF over denominator 100 end fraction rightwards double arrow space space space 1 half equals fraction numerator 20 plus EF over denominator 100 end fraction space space space space left square bracket therefore space BE space equals space CD space equals space 20 straight m right square bracket
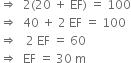
rightwards double arrow space space 2 left parenthesis 20 space plus space EF right parenthesis space equals space 100 rightwards double arrow space space 40 space plus space 2 space EF space equals space 100 rightwards double arrow space space space 2 space EF space equals space 60 rightwards double arrow space space EF space equals space 30 space straight m

Let DF be the length of the second kite.
Now, in right triangle DEF, we have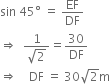
sin space 45 degree space equals space EF over DF rightwards double arrow space space fraction numerator 1 over denominator square root of 2 end fraction equals 30 over DF rightwards double arrow space space space space DF space equals space 30 square root of 2 straight m
Hence, the length of te string = 30 square root of 2 straight m.
Hence, the usual speed of the aircraft be x km/hr = 750 km/hr.

Some More Questions From Circles Chapter

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation