A TV tower stands vertically on a bank of a canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point 20 m away from this point on the line joing this point to the foot of the tower, the angle of elevation of the top of the tower is 30° (see Fig. 9.12). Find the height of the tower and the width of the canal.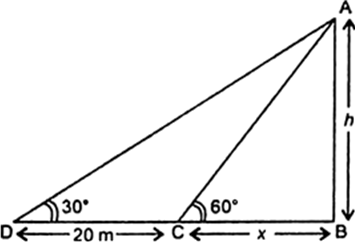
Fig. 9.12.
Let AB be the tower of height h metres standing on a bank of a canal. Let C be a point on the opposite bank of a canal, such that BC = x metres.
Let D be the new position after changing the elevation. It is given that CD = 20 m
The angle of elevation of the top of the tower at C and D are respectively 60° and 30°.
i.e. ∠ACB = 60° and ∠ADB = 30°
In right triangle ABC, we have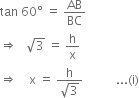
In right triangle ABD, we have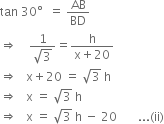
Comparing (i) and (ii), we get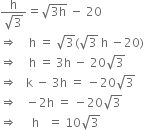
Putting this value in (i), we get
Hence, the height of tower 
metres and width of the canal = 10 m.
