Question
Prove the following identity:![]()
Solution
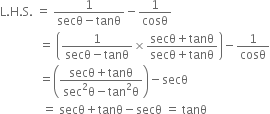

Hence, L.H.S. = R.H.S.
Prove the following identity:![]()
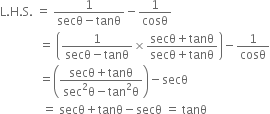

Choose the correct option and justify your choice:
sin 2A = 2 sin A is true when A =
(A) 0° (B) 30° (C) 45° (D) 60°
Mock Test Series