Question
Prove the following identity:
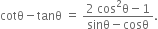
Solution
L.H.S. =
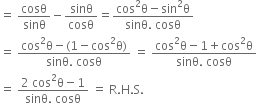
Hence, L.H.S. = R.H.S.
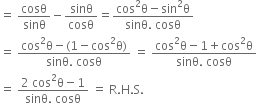
Mock Test Series