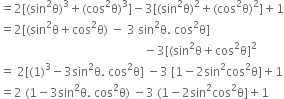Question
Prove the following identity:
2 (sin6θ + cos6θ) -3 (sin4θ + cos4θ) + 1 = 0
Solution
L.H..S. = ![]()