Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.

Let the length of the garden be x m and width bey m.

Case I.    x = y + 4

⇒    x - y = 4

Case II.

Half perimeter = 36

⇒    x + y =36

So algebraic representation be

x - y = 4

x + y = 36

Graphical representation :

We have, x - y = 4

⇒    x = 4 + y

Thus, we have following table

x + y = 36

⇒    x = 36 - y

Thus, we have following table :

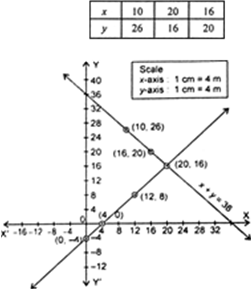
Fig. 3.10.
If we plot the graph of both the equations, we find that the two lines intersect at the point (20, 16). So, x = 20, y = 16 is the required solution of the given equation i.e., the length of the garden is 20 m and breadth be 16 m.