+91-8076753736[email protected]
logo
logo
-->

Arithmetic Progressions

Question
CBSEENMA10007993
Wired Faculty App

Split 69 into three parts such that they are in A .P. and the product of two smaller parts is 483.

Solution

Let the three parts, which are in A .P. be a – d, a, a + d
Case I.
a – d + a + a + d = 69
⇒ 3a = 69
a = 23 ...(i)
Case II. a (a – d) = 483 ...(ii)
Putting the value of (i) in (ii), we get
23 (23 - d)  = 483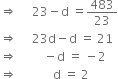
rightwards double arrow space space space space space 23 minus straight d space equals 483 over 23 rightwards double arrow space space space space space 23 straight d minus straight d space equals space 21 rightwards double arrow space space space space space space space space space minus straight d space equals space minus 2 rightwards double arrow space space space space space space space space space space space space straight d space equals space 2
Thus, the three parts are
  a - d = 23 - 2 = 21 
      a  = 23
and     a + d = 23 + 2 = 25

Some More Questions From Arithmetic Progressions Chapter

In which of the following situational, does the list of numbers involved make an arithmetic progression, and why?

The cost of digging a well for the first metre is Rs. 150 and rises by Rs. 50 for each succeeding metre.

Write first four terms of the AP, when the first term a and the common difference d are given as follows:
a – 10, d = 10

Write first four terms of the AP, when the first term a and the common difference d are given as follows:
a = –2, d = 0

Write first four terms of the AP, when the first term a and the common difference d are given as follows:
a = 4, d = – 3

Write first four terms of the AP, when the first term a and the common difference d are given as follows:

a = – 1.25, d = – 0.25

For the following APs, write the first term and the common difference
3, 1, – 1, – 3, . . .

For the following APs, write the first term and the common difference
– 5, – 1, 3, 7, . . .

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation