Prove the following identities:
$secA space left parenthesis 1 minus sinA right parenthesis thin space left parenthesis secA plus tanA right parenthesis space equals 1.$

Solution

sec A (1 - sin A) (sec A + tan A) = 1
L.H.S. = sec A (1 - sin A) (sec A + tan A)
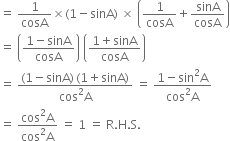
$equals space 1 over cosA cross times left parenthesis 1 minus sinA right parenthesis space cross times space open parentheses 1 over cosA plus sinA over cosA close parentheses equals space open parentheses fraction numerator 1 minus sinA over denominator cosA end fraction close parentheses space open parentheses fraction numerator 1 plus sinA over denominator cosA end fraction close parentheses equals space fraction numerator left parenthesis 1 minus sinA right parenthesis thin space left parenthesis 1 plus sinA right parenthesis over denominator cos squared straight A end fraction space equals space fraction numerator 1 minus sin squared straight A over denominator cos squared straight A end fraction equals space fraction numerator cos squared straight A over denominator cos squared straight A end fraction space equals space 1 space equals space straight R. straight H. straight S.$
Hence, L.H.S. = R.H.S.

For Daily Free Study Material Join wiredfaculty

Some Applications Of Trigonometry

Prove the following identities:
$secA space left parenthesis 1 minus sinA right parenthesis thin space left parenthesis secA plus tanA right parenthesis space equals 1.$

Some More Questions From Some Applications of Trigonometry Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction