Find the value of sin 30° geometrically.

Solution

Consider an equilateral ΔABC.
Since each angle in a equilateral A is 60°.
∴ ∠A = ∠B = ∠C = 60°
Draw a perpendicular from A on side BC.
Now, ΔABD= ΔACD => BD = DC
and ΔBAD = ΔCAD [C.P.C.T.]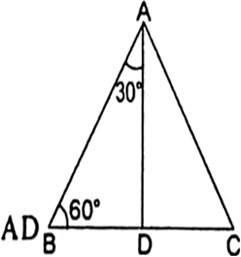

Let AB = 2a. Then, $BD space equals space 1 half BC space equals space straight a$
In right ΔADB, by Pythagoras theorem.
$AD squared plus BD squared space equals space AB squared space space rightwards double arrow space space AD squared space equals space AB squared minus BD squared space equals space left parenthesis 2 straight a right parenthesis squared minus straight a squared space equals 3 straight a squared space rightwards double arrow space space space AD squared space equals space 3 straight a squared space rightwards double arrow space space AD space equals space straight a square root of 3$
Now, in right ΔADB,
$sin space 30 degree space equals space BD over AB equals fraction numerator straight a over denominator 2 straight a end fraction equals 1 half.$

For Daily Free Study Material Join wiredfaculty

Some Applications Of Trigonometry

Find the value of sin 30° geometrically.

Some More Questions From Some Applications of Trigonometry Chapter

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction