Question
If ![]() find the value of (sinA + cosA) secA.
find the value of (sinA + cosA) secA.
Solution
Let us consider a right triangle right angled at B.
We have,
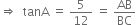
If AB = 5K, BC = 12K
Then,

So, AC = 13K
Now,
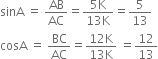

Therefore,
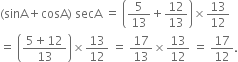
We have,
If AB = 5K, BC = 12K
Then,
So, AC = 13K
Now,
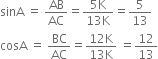
Therefore,