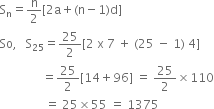+91-8076753736[email protected]
logo
logo
-->

Arithmetic Progressions

Question
CBSEENMA10007877
Wired Faculty App

Show that a1 , a2 , . . ., an, . . . form an AP where an is defined as below :
an = 3 + 4n

Solution

It is given that,
         an = 3 + 4n
So,    a1 = 3 + 4(1) = 3 + 4 = 7
         a2  = 3 + 4 (2) = 3 + 8 = 11
and    a3 = 3 + 4(3) = 3 + 12 = 15
Now, er have following numbers :
    7, 11, 15, ...........
Since the difference between each pair of consecutive terms are constant
So, the given number forms an A. P.
Here, a = 7, d = 4,    n  = 15
We know that, 
straight S subscript straight n equals straight n over 2 left square bracket 2 straight a plus left parenthesis straight n minus 1 right parenthesis straight d right square bracket So comma space space space straight S subscript 25 equals 25 over 2 left square bracket 2 space straight x space 7 space plus space left parenthesis 25 space minus space 1 right parenthesis space 4 right square bracket space space space space space space space space space space space space space space equals 25 over 2 left square bracket 14 plus 96 right square bracket space equals space 25 over 2 cross times 110 space space space space space space space space space space space space space space space equals space 25 cross times 55 space equals space 1375

Some More Questions From Arithmetic Progressions Chapter

Write first four terms of the AP, when the first term a and the common difference d are given as follows:
a = –2, d = 0

Write first four terms of the AP, when the first term a and the common difference d are given as follows:
a = 4, d = – 3

Write first four terms of the AP, when the first term a and the common difference d are given as follows:

a = – 1.25, d = – 0.25

For the following APs, write the first term and the common difference
3, 1, – 1, – 3, . . .

For the following APs, write the first term and the common difference
– 5, – 1, 3, 7, . . .

For the following APs, write the first term and the common difference
0.6, 1.7, 2.8, 3.9, . . .

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation