In an AP
Given a = 5, d = 3, an =50, find n and Sn.
Here a = 5, d = 3, an = 50
We know that, an = a + (n – 1 )d
⇒ 50 = 5 + (n – 1) x 3
⇒ 50 – 5 = 3 x (n – 1)
⇒ 45 = 3 x (n – 1)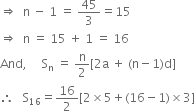
= 8 x [ 10 + 15 x 3]
= 8 x 10 + 45
= 8 x 55 = 440
Hence, n = 16
and Sn =S16 = 440
In which of the following situations, does the list of numbers involved make an arithmetic progression, and why?
The taxi fare after each km when the fare is Rs. 15 for the first km and Rs. 8 for each additional km.
Write first four terms of the AP, when the first term a and the common difference d are given as follows:
a – 10, d = 10
Write first four terms of the AP, when the first term a and the common difference d are given as follows:
a = –2, d = 0
Write first four terms of the AP, when the first term a and the common difference d are given as follows:
a = 4, d = – 3
Mock Test Series
