+91-8076753736[email protected]
logo
logo
-->

Coordinate Geometry

Question
CBSEENMA9001789
Wired Faculty App

For what value of a the polynomial 2x3 + ax2 + 11x + a + 3 is exactly divisible by 2x - 1?

Solution

Let p(x) = 2x3 + ax2 + 11x + a + 3
If p(x) is exactly divisible by 2x - 1, then by factor theorem,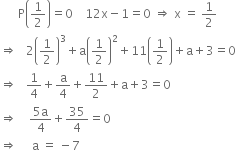
space space space space space space straight P open parentheses 1 half close parentheses equals 0 space space space space 12 straight x minus 1 equals 0 space rightwards double arrow space straight x space equals space 1 half rightwards double arrow space space space 2 open parentheses 1 half close parentheses cubed plus straight a open parentheses 1 half close parentheses squared plus 11 open parentheses 1 half close parentheses plus straight a plus 3 equals 0 rightwards double arrow space space space 1 fourth plus straight a over 4 plus 11 over 2 plus straight a plus 3 equals 0 rightwards double arrow space space space space fraction numerator 5 straight a over denominator 4 end fraction plus 35 over 4 equals 0 rightwards double arrow space space space space space straight a space equals space minus 7

Hence, the required polynomial is
2x3 - 7x2 + 11x - 7 + 3
or 2x3 - 7x2 + 11x - 4

Some More Questions From Coordinate Geometry Chapter

Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.

4x2 - 3x + 7

Which of the following expressions are polynomials in one variable and which are not? State reasons for your answer.

x10+ y3 + t50

Write the coefficients of x2 in each of the following:

2 + x2 + x

Write the coefficients of x2 in each of the following:
2 - x2 + x3

Mock Test Series

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation