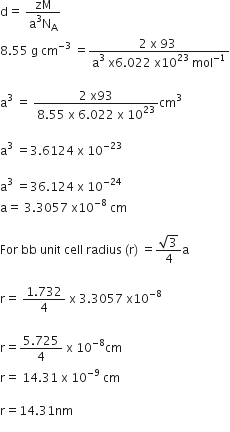The Solid State

Question

Wired Faculty App

Niobium crystallises in body centered cubic structure. If density is 8.55 g cm^–3, calculate atomic radius of niobium using its atomic mass 93 u.

Solution

We have give that,
Density (d)=8.55 g Cm^-3
Atomic mass (M) =93u =93 gMol^-1
Atomic radius (r) = ?

We know that, Avogadro number N_a =6.022 x 10 ²³ mol^-1

since given lattice is bcc

therefore
Number of atoms per unit cell (z) =2

we know that

straight d equals space fraction numerator zM over denominator straight a cubed straight N subscript straight A end fraction 8.55 space straight g space cm to the power of negative 3 end exponent space equals fraction numerator 2 space straight x space 93 space over denominator straight a cubed space straight x 6.022 space straight x 10 to the power of 23 space mol to the power of negative 1 end exponent end fraction straight a cubed space equals space fraction numerator 2 space straight x 93 over denominator 8.55 space straight x space 6.022 space straight x space 10 to the power of 23 end fraction cm cubed straight a cubed space equals 3.6124 space straight x space 10 to the power of negative 23 end exponent straight a cubed space equals 36.124 space straight x space 10 to the power of negative 24 end exponent straight a equals space 3.3057 space straight x 10 to the power of negative 8 end exponent space cm For space bb space unit space cell space radius space left parenthesis straight r right parenthesis space equals fraction numerator square root of 3 over denominator 4 end fraction straight a straight r equals space fraction numerator 1.732 over denominator 4 end fraction space straight x space 3.3057 space straight x 10 to the power of negative 8 end exponent straight r equals fraction numerator 5.725 over denominator 4 end fraction space straight x space 10 to the power of negative 8 end exponent cm straight r equals space 14.31 space straight x space 10 to the power of negative 9 end exponent space cm straight r equals 14.31 nm

Some More Questions From The Solid State Chapter

Classify the following as amorphous or crystalline solids: Polyurethane, naphthalene, benzoic acid, teflon, potassium nitrate, cellophane, polyvinyl chloride, fibre glass, copper.

Why is glass considred a super-cooled liquid?

Refractive index of a solid is observed to have the same value along all directions. Comment on the nature of this solid. Would it show clevage property?

Classify the following solids in different categories based on the nature of intermolecular forces operating in them:
Potassium sulphate, tin, benzene, urea, ammonia, water, zinc
sulphate, graphite, rubidium, argon, silicon carbide.

For Daily Free Study Material Join wiredfaculty

The Solid State

Niobium crystallises in body centered cubic structure. If density is 8.55 g cm^–3, calculate atomic radius of niobium using its atomic mass 93 u.

Some More Questions From The Solid State Chapter

Classify the following as amorphous or crystalline solids: Polyurethane, naphthalene, benzoic acid, teflon, potassium nitrate, cellophane, polyvinyl chloride, fibre glass, copper.

Why is glass considred a super-cooled liquid?

Refractive index of a solid is observed to have the same value along all directions. Comment on the nature of this solid. Would it show clevage property?

Classify the following solids in different categories based on the nature of intermolecular forces operating in them:
Potassium sulphate, tin, benzene, urea, ammonia, water, zinc
sulphate, graphite, rubidium, argon, silicon carbide.

Solid A is a very hard, electrical insulator in solid as well as in molten state and melts at extremely high temperature. What type of solid is it?

Ionic solids conduct electricity in liquid state but not in solid state. Explain.

What type of solids are electrical conductors, malleable and ductile?

Give the significance of a 'lattice point'.

Name the parameters that characterize a unit cell.

Distinguish between Hexagonal and monoclinic unit cells.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

The Solid State

Niobium crystallises in body centered cubic structure. If density is 8.55 g cm–3, calculate atomic radius of niobium using its atomic mass 93 u.

Some More Questions From The Solid State Chapter

Classify the following as amorphous or crystalline solids: Polyurethane, naphthalene, benzoic acid, teflon, potassium nitrate, cellophane, polyvinyl chloride, fibre glass, copper.

Why is glass considred a super-cooled liquid?

Refractive index of a solid is observed to have the same value along all directions. Comment on the nature of this solid. Would it show clevage property?

Classify the following solids in different categories based on the nature of intermolecular forces operating in them: Potassium sulphate, tin, benzene, urea, ammonia, water, zinc sulphate, graphite, rubidium, argon, silicon carbide.

Solid A is a very hard, electrical insulator in solid as well as in molten state and melts at extremely high temperature. What type of solid is it?

Ionic solids conduct electricity in liquid state but not in solid state. Explain.

What type of solids are electrical conductors, malleable and ductile?

Give the significance of a 'lattice point'.

Name the parameters that characterize a unit cell.

Distinguish between Hexagonal and monoclinic unit cells.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Niobium crystallises in body centered cubic structure. If density is 8.55 g cm^–3, calculate atomic radius of niobium using its atomic mass 93 u.

Classify the following solids in different categories based on the nature of intermolecular forces operating in them:
Potassium sulphate, tin, benzene, urea, ammonia, water, zinc
sulphate, graphite, rubidium, argon, silicon carbide.