Question
With the help of a ray diagram obtain the expression for the magnifying power of a simple microscope when the image is formed at the least distance of distinct vision.
Solution
Image is formed at the near point.
Magnifying Power (Angular Magnification). Magnifying power (M) is the ratio of the angle subtended at the eye by the image at the near-point, to the angle subtended at an unaided eye by the object, at the least distance of distinct vision.
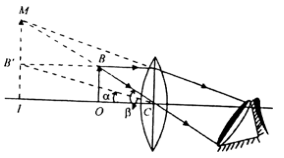
In figure the image is formed at the near point.
Let the angle subtended by the image at the near point at the eye be β. If the object is kept at the near point [marked as IE in figure], then the angle subtended by the object at the eye is,

Hence when the simple microscope is adjusted such that the image is formed at the near point, the angular magnification is equal to the linear magnification.
Applying new cartesian sign convention, u is -ve, v is -ve and f is +ve.
The lens equation is,
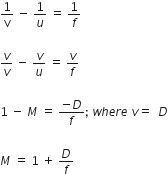
This is the required expression for magnification.
Magnifying Power (Angular Magnification). Magnifying power (M) is the ratio of the angle subtended at the eye by the image at the near-point, to the angle subtended at an unaided eye by the object, at the least distance of distinct vision.

In figure the image is formed at the near point.
Let the angle subtended by the image at the near point at the eye be β. If the object is kept at the near point [marked as IE in figure], then the angle subtended by the object at the eye is,

Hence when the simple microscope is adjusted such that the image is formed at the near point, the angular magnification is equal to the linear magnification.
Applying new cartesian sign convention, u is -ve, v is -ve and f is +ve.
The lens equation is,
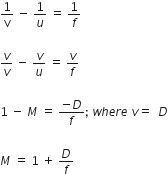
This is the required expression for magnification.



