SSCCHSL quantitative aptitude
Sponsor Area
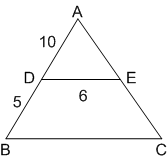
In ΔABC, D and E are points on side AB and AC respectively. DE is parallel to BC. If lengths of AD, DB and DE are 10 cm, 5 cm and 6 cm respectively. What is the length of BC?
9 cm
2 cm
3 cm
11 cm
A.
9 cm
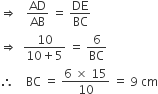
Sponsor Area
A carpenter can build a cupboard in 60 hours. After 15 hours he takes a break. What fraction of the cupboard is yet to be built?
0.5
0.9
0.75
0.25
C.
0.75
Carpenter takes break after 15 hours
∴ 45 hours of work is left
∴ Fraction of work left
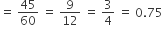
Which of the following equations has the sum of its roots?
x2 - 5x + 6 = 0
x2 - 5x - 6 = 0
x2 + 5x + 6 = 0
x2 + 5x - 6 = 0
A.
x2 - 5x + 6 = 0
x2 - 5x + 6 = 0
The sum of roots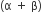 
is given by,
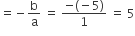
If Girilal's salary is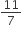 
times of Hariram's and Shekhar's is 
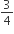times of Hariram's, What is the ratio of Girilal's salary to Shekhar's salary.
44 : 21
28 : 33
33 : 28
21 : 44
A.
44 : 21
Girilal =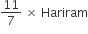 
7Girilal = 11 Hariram
∴ Girilal : Hariram = 11 : 7 ...(i)
Hariram : Shekhar = 4 : 3 ...(ii)
∴ Girilal : Hariram : Shekhar = 11 x 4 : 7 x 4 : 7 x 3
= 44 : 28 : 21
(cos A + sin A)2 + (cos A - sin A)2 equals to
1
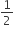
2
0
C.
2
[cos A + sin A]2 + [cos A - sin A]2
= cos2A + sin2A + 2cosAsinA + cos2A +sin2A - 2cosA sinA
= 1 + 1 = 2
Sponsor Area
Mock Test Series
Mock Test Series