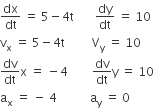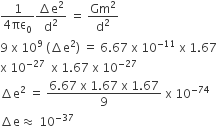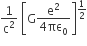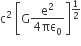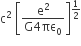One end of a string of length l is connected to a particle of mass ‘m’ and the other end is connected to a small peg on a smooth horizontal table. If the particle moves in circle with speed ‘v’, the net force on the particle (directed towards centre) will be (T represents the tension in the string)
-
T
-
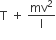
-
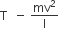
-
zero
A.
T
Centripetal force mv2/l is provided by tension so the net force will be equal to tension i.e., T.