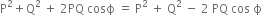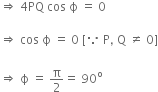Question
At what height from the surface of earth the gravitation potential and the value of g are -5.4 x 107 J kg-2 and 6.0 m/s2 respectively? (Take the radius of the earth as 6400 km)
-
1600 km
-
1400 km
-
2000 km
-
2600 km
Solution
D.
2600 km
Gravitational potential at some height h from the surface of the earth is given by,
V = 
... (i)
Acceleration due to gravity at some height h from the earth surface can be given as,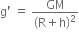
... (ii)
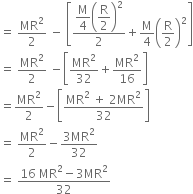
From equation (i) and (ii), we get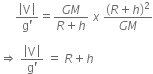
... (iii)
V = -54 x 107 J kg-2
g' = 6.0 m/s2
Radius of Earth, R = 6400 km
Putting the values in Eqn. (iii), we get
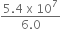= R+h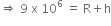
h = (9-6.4)x106 = 2.6 x 106 m
h = 2600 km
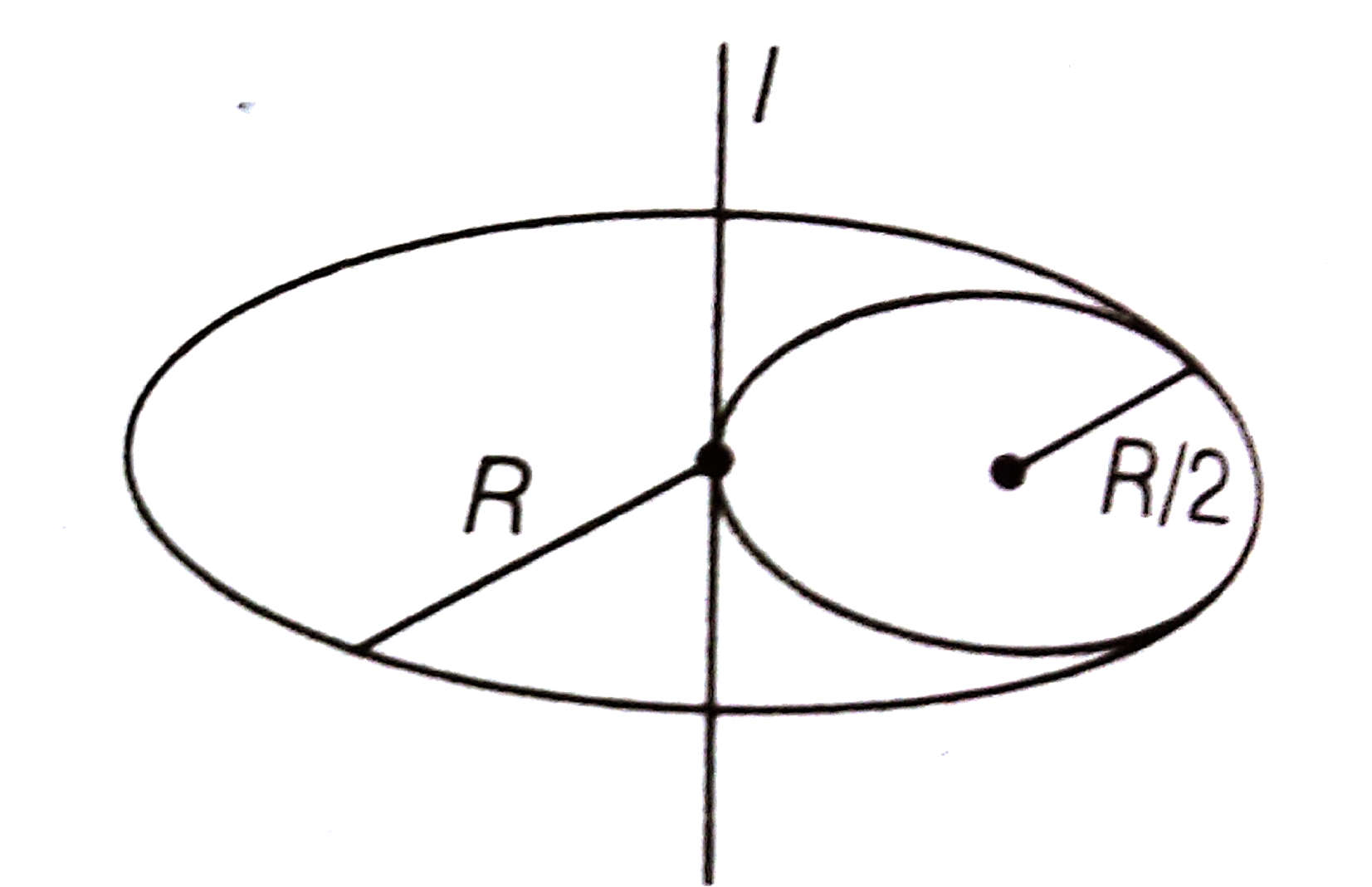
. The coefficient of friction between the tyres of the car and the road is 
. The maximum safe velocity on this road is,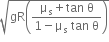
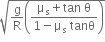
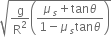
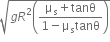
and the coefficient of friction between the tyres of car and the road is 
.
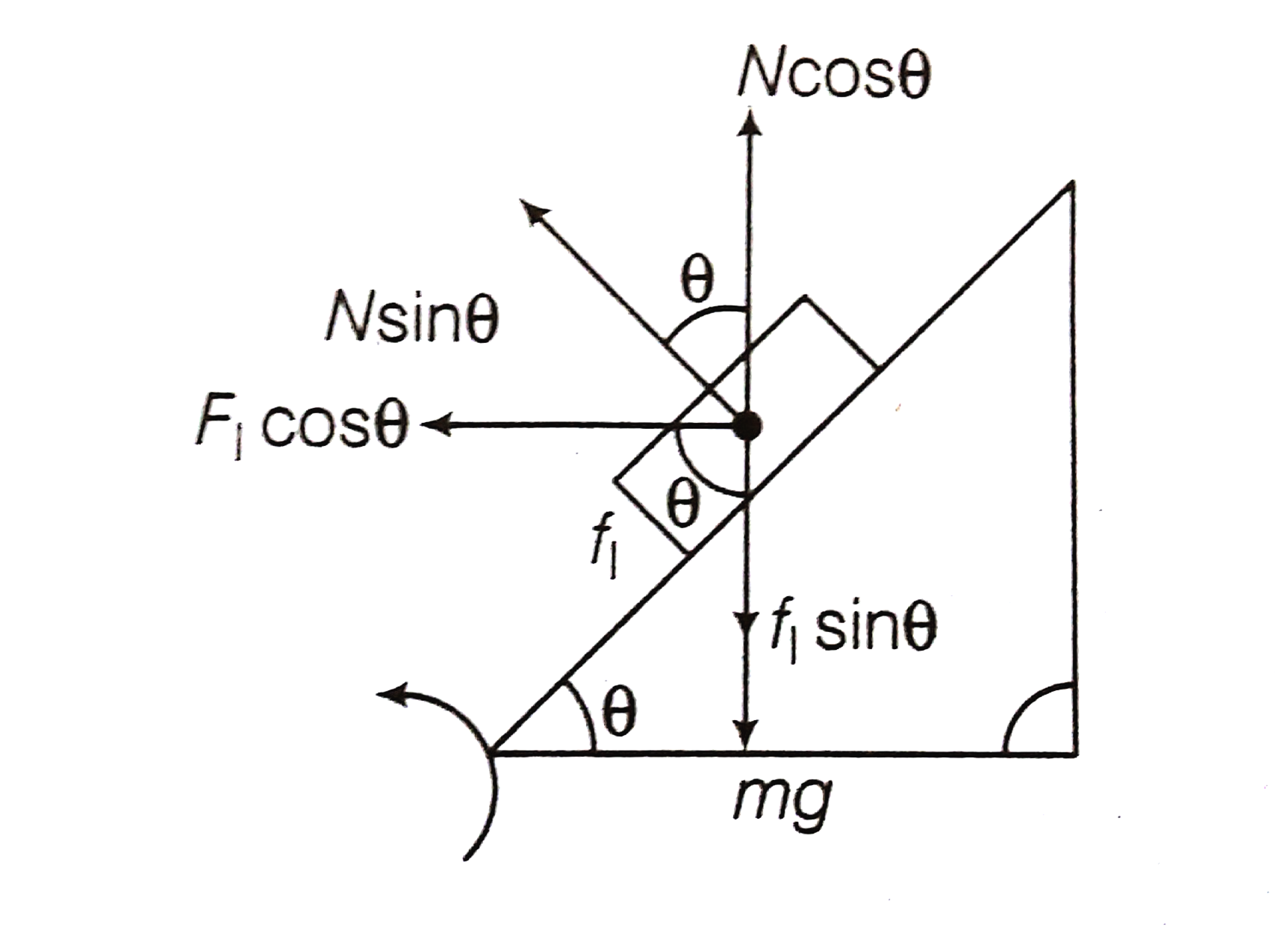
= mg + f1 sin 
mg = N cos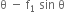 
... (i)
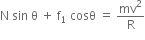... (ii)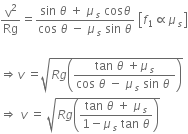
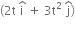N, where 
are units vectors along X and Y axis. What power will be developed by the force at the time (t)?
+3t2 
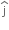) N,
are unit vectors along X and Y axis.
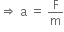
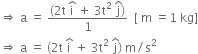
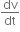
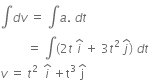
+ 3t2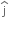 
).(
)
,
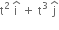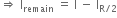
