The additional kinetic energy to be provided to a satellite of mass m revolving around a planet of mass M, to transfer it from a circular orbit of radius R1 to another of radius R2(R2> R1) is
D.
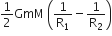
The kinetic energy changing the orbit of satellite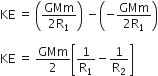
Sponsor Area
The additional kinetic energy to be provided to a satellite of mass m revolving around a planet of mass M, to transfer it from a circular orbit of radius R1 to another of radius R2(R2> R1) is

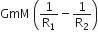
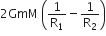
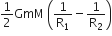
D.
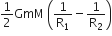
The kinetic energy changing the orbit of satellite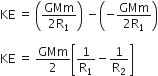
Sponsor Area
The speed of the projectile at its maximum height is half of its initial speed. The angle of projection is
60o
15o
30o
45o
A.
60o
The speed of projectile at its maximum height
v' = vo cos θ
vo/2 = vo cos θ
cos θ = 1/2
θ = 60o
From a circular disc of radius R and mass 9M, a small disc of mass M and radius R/3 is removed concentrically. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through its centre is
40MR2/9
MR2
4 MR2
4MR2/9
A.
40MR2/9
The moment of inertia of the remaining disc about axis perpendicular to the plane of the disc and passing through its centre.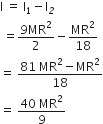
A particle moves in the x-y plane according to rule x = a sin ωt and y = a cos ωt. The particle follows
an elliptical path
a circular path
a parabolic path
a straight line path inclined equally to x and y- axes
B.
a circular path

A closely wound solenoid of 2000 turns and area of cross -section 1.5 x 10-4 m2 carries a current of 2.0 A. It is suspended through its centre and perpendicular to its length, allowing it to turn in a horizontal plane in a uniform magnetic field 5 x 10-2 T making an angle of 30o with axis of the solenoid. The torque on the solenoid will be
3 x 10-3 N-m
1.5 x 10-3 N-m
1.5 x 10-2 N-m
3 x 10-2 N-m
A.
3 x 10-3 N-m
Given, N = 2000,
A = 1.5 x 10-4 m2
i = 2.0 A B = 5 x 10-2 T
and
θ = 30o
Torque = NiBA sin θ
2000 x 2 x 5 x 10-2 x 1.5 x 10-14 x sin 30o
= 2000 x 50 x 10-6 x (1/2)
= 1.5 x 10-2 Nm
Sponsor Area
Mock Test Series