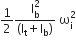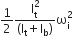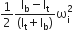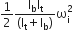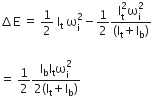A block of mass m is in contact with the cart C as shown in the figure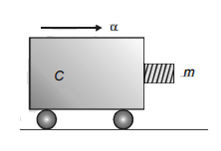
The coefficient of static friction between the block and the cart is μ. The acceleration α of the cart that will prevent the block from falling satisfies
C.
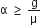
When a cart moves with some acceleration toward right then a pseudo force (mα) acts on block towards left. The force (mα) is action force by a block on the cart. Now, block will remain static w.r.t cart if frictional force 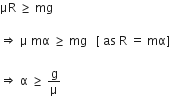





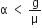



 Another disk of moment of inertia Ib is dropped coaxially onto the rotating disk. Initially, the second disk has zero angular speed. Eventually, both the disks rotate with constant angular speed.
Another disk of moment of inertia Ib is dropped coaxially onto the rotating disk. Initially, the second disk has zero angular speed. Eventually, both the disks rotate with constant angular speed. The energy lost by the initially rotating disc due to friction is
The energy lost by the initially rotating disc due to friction is