The position x of a particle with respect to time t along x- axis is given by x = 9t2 -t3 where x is in meter and t in second. What will be the position of this particle when it achieves maximum speed along the +x direction?
-
32 m
-
54 m
-
81 m
-
24 m
B.
54 m
At the instant when speed is maximum, its acceleration is zero.
Given, the position x of particle with respect to time t along x- axis
x = 9t2-t3 ... (i)
differentiating Eq. (i) with respect to time, we get speed, ie, 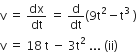
Again differentiating Eq. (ii) with respect to time, we get acceleration, ie, 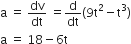
Now, when speed of particle is maximum, its acceleration is zero, ie,
a= 0
18-6t = 0 or t = 3s
Putting in eq (i) We, obtain the position of a particle at that time.
x = 9 (3)2 - (3)3 = 9 (9) -27
= 81-27 = 54 m






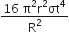
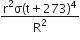

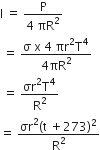
 ). The path of the particle makes with the x -axis an angle of:
). The path of the particle makes with the x -axis an angle of: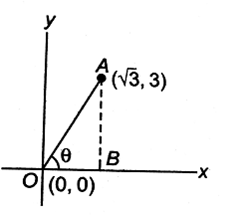
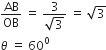
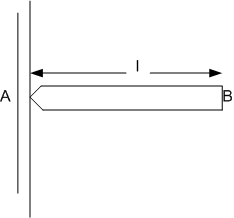
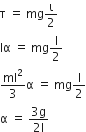 length.
length.