Question

Two masses m₁ = 5 kg and m₂ = 10 kg, connected by an inextensible string over a frictionless pulley, are moving as shown in the figure. The coefficient of friction of the horizontal surface is 0.15. The minimum weight m that should be put on top of m₂ to stop the motion is :

10.3 kg

18.3 kg

27.3 kg

43.3 kg

Solution

C.

27.3 kg

Given: m₁ = 5kg;
m₂ = 10 kg
μ = 0.15
For m₁, m₁g -T =m₁a
= 50-T = 5 x a
and T - 0.15 (m+10) g = (10 + m)a
For rest a = 0
or 50 = 0.15 (m +10) 10

$\Rightarrow 5 = \frac{3}{20} (m + 10) \frac{100}{3} = m + 10 m = 23.3 k g$

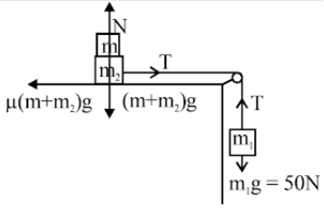
The minimum value from the options, satisfying the above condition is, m = 27.3 kg

Question

Wired Faculty App

In a collinear collision, a particle with an initial speed v0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after the collision, is:

$\frac{ν_{o}}{\sqrt{2}}$

v_o/4

$\sqrt{2} v_{0}$

v₀/2

Solution

C.

$\sqrt{2} v_{0}$

$\frac{1}{2} m v_{1}^{2} + \frac{1}{2} m v_{2}^{2} = \frac{3}{2} (\frac{1}{2} m v_{0}^{2}) \Rightarrow v_{1}^{2} + v_{2}^{2} = \frac{3}{2} v_{0}^{2} . . . . (i) F r o m m o m e n t u m c o n s e r v a t i o n m v_{0} = m (v_{1} + v_{2}) . . . (i i) S q u a r r i n g b o t h s i d e s, (v_{1} + v_{2})^{2} = v_{0}^{2} \Rightarrow v_{1}^{2} + v_{2}^{2} + 2 v_{1} v_{2} = v_{0}^{2} 2 v_{1} v_{2} = - \frac{v_{0}^{2}}{2} (v_{1} - v_{2})^{2} = v_{1}^{2} + v_{2}^{2} - 2 v_{1} v_{2} = \frac{3}{2} v_{0}^{2} + \frac{v_{0}^{2}}{2}$

solving we get relative velocity between the two particles

$v_{1} - v_{2} = \sqrt{2 v_{0}}$

Question

Wired Faculty App

A particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the n^th power of R. If the period of rotation of the particle is T, then:

$T \propto R^{n / 2}$

$T \propto R^{3 / 2} f o r a n y n$

$T \propto R^{\frac{n}{2} + 1}$

$T \propto R^{\frac{n + 1}{2}}$

Solution

D.

$T \propto R^{\frac{n + 1}{2}}$

$m ω^{2} R = F o r c e \propto \frac{1}{R^{n}} (F o r c e = \frac{m v^{2}}{R}) \Rightarrow ω^{2} \propto \frac{1}{R^{n + 1}} \Rightarrow ω \propto \frac{1}{R^{\frac{n + 1}{2}}} T i m e P e r i o d T = \frac{2 π}{ω} T i m e P e r i o d T \propto R^{\frac{n + 1}{2}}$

Question

Wired Faculty App

It is found that if a neutron suffers an elastic collinear collision with deuterium at rest, fractional loss of its energy is p_d; while for its similar collision with carbon nucleus at rest, fractional loss of energy is p_c. The values of p_d and p_c are respectively :

(0,1)

(.89,.28)

(.28,.89)

(0,0)

Solution

B.

(.89,.28)

For collision of a neutron with deuterium:

Applying conservation of momentum:

mv + 0 = mv₁ + 2mv₂ .....(i)
v₂ -v₁ = v ...... (ii)

Therefore, Collision is elastic, e = 1

From equ (i) and equ (ii) v₁ = -v/3

$P_{d} = \frac{\frac{1}{2} m v^{2} - \frac{1}{2} m v_{1}^{2}}{\frac{1}{2} m v^{2}} = \frac{8}{9} = 0.89$

Now, for the collision of neutron with carbon nucleus

Applying conservation of momentum

mv + 0 = mv₁ + 12mv₂ ....; (iii)

v = v₂-v₁ ....(iv)

$v_{1} = - \frac{11}{13} v P_{c} = \frac{\frac{1}{2} m v^{2} - \frac{1}{2} m {(\frac{11}{13} v)}^{2}}{\frac{1}{2} m v^{2}} = \frac{48}{169} \approx 0.28$

Question

Wired Faculty App

All the graphs below are intended to represent the same motion. One of them does it incorrectly. Pick it up.

Solution

C.

For Daily Free Study Material Join wiredfaculty

WhatsApp Group

Download Android App

Ncert Book Download

JEE physics

All the graphs below are intended to represent the same motion. One of them does it incorrectly. Pick it up.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation

Phone Number

Email Address

Loaction

For Daily Free Study Material Join wiredfaculty

WhatsApp Group

Download Android App

Ncert Book Download

JEE physics

A particle is moving with a uniform speed in a circular orbit of radius R in a central force inversely proportional to the nth power of R. If the period of rotation of the particle is T, then: T∝ Rn/2 T∝ R3/2 for any n T∝Rn2+1 T∝ Rn+12

It is found that if a neutron suffers an elastic collinear collision with deuterium at rest, fractional loss of its energy is pd; while for its similar collision with carbon nucleus at rest, fractional loss of energy is pc. The values of pd and pc are respectively : (0,1) (.89,.28) (.28,.89) (0,0)

All the graphs below are intended to represent the same motion. One of them does it incorrectly. Pick it up.

Mock Test Series

NCERT Sample Papers

Entrance Exams Preparation