Sponsor Area
A particle of mass m is moving along the side of a square of side ‘a’, with a uniform speed v in the x-y plane as shown in the figure: 
Which of the following statements is false for the angular momentum → L about the origin?
B.
For a particle of mass, m is moving along the side of a square a. Such that
Angular momentum L about the origin
Sponsor Area
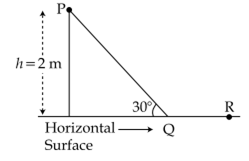
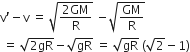A point particle of mass m, moves along the uniformly rough track PQR as shown in the figure. The coefficient of friction, between the particle and the rough track equals µ. The particle is released, from rest, from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR. The values of the coefficient of friction µ and the distance x(=QR), are, respectively close to :
0.2 and 6.5 m
0.2 and 3.5 m
0.29 and 3.5 m
0.29 and 6.5 m
C.
0.29 and 3.5 m
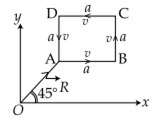
Energy lost over path PQ = μ mg cos θ x 4
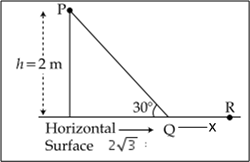
Energy lost over path QR = μ mgx
i.e μ mg cos 30° x 4 = μ mgx (∴ θ = 30°)
From Q to R energy loss is half of the total energy loss.
i.e μ mgx = mgh/2
μ = 0.29
The values of the coefficient of friction μ and the distance x (=OR) are 0.29 and 3.5 m
A person trying to lose weight by burning fat lifts a mass of 10 kg upto a height of 1 m 1000 times. Assume that the potential energy lost each time he lowers the mass is dissipated. How much fat will he use up considering the work done only when the weight is lifted up ? Fat supplies 3.8×107 J of energy per kg which is converted to mechanical energy with a 20% efficiency rate. Take g=9.8 ms−2:
2.45 ×10−3 kg
6.45 x×10−3 kg
9.89 ×10−3 kg
12.89 ×10−3 kg
D.
12.89 ×10−3 kg
Given potential energy burnt by lifting weight
= mgh = 10 x 9.8 x 1 x 1000 = 9.8 x 104 J
If mass lost by a person be m, then energy dissipated
= m x 2 x 38 x 107 J /10
⇒ m = 5 x 10-3 x 9.8 / 3.8
= 12.89 x 10-3 kg
A roller is made by joining together two cones at their vertices O. It is kept on two rails AB and CD which are placed asymmetrically (see figure), with its axis perpendicular to CD and its centre O at the centre of line joining AB and CD (see figure). It is given a light push so that it starts rolling with its centre O moving parallel to CD in the direction shown. As it moves, the roller will tend to:
turn left
turn right
go straight
turn left and right alternately
A.
turn left
As, the wheel rolls forward the radius of the wheel, decreases along AB hence for the same number of rotations it moves less distance along AB, hence it turns left.
A satellite is revolving in a circular orbit at a height ‘h’ from the earth’s surface (radius of earth R ; h<<R). The minimum increase in its orbital velocity required, so that the satellite could escape from the earth’s gravitational field, is close to: (Neglect the effect of atmosphere.)
D.
Given, a satellite is revolving in a circular orbit at a height h from the Earth's surface having radius of earth R, i.e h <<R
Orbit velocity of a satellite
therefore, the minimum increase in its orbital velocity required to escape from the Earth's Gravitational Field.
Sponsor Area
Mock Test Series
