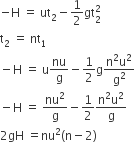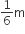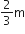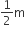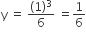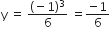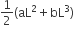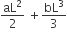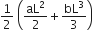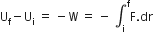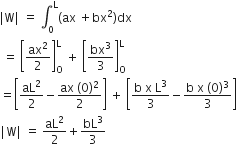From the tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle to hit the ground is n times that taken by it to reach the highest point of its path. The relation between H,u and n is

• 2gH = n²u²

• gH = (n-2)²u²

• 2gH = nu²(n-2)²u²

• gH = (n-2)²u²

A mass ‘m’ is supported by a massless string wound around a uniform hollow cylinder of mass m and radius R. If the string does not slip on the cylinder, with what acceleration will the mass fall on release?

• 2g/3

• g/2

• 5g/6

• g

A block of mass m is placed on a surface with a vertical cross-section given by y = x³/6. If the coefficient of friction is 0.5, the maximum height above ground at which the block can be placed without slipping is 

• 
• 
• 
• 

A.

A block of mass m is placed on a surface with vertical cross section, then


At limiting equilibrium, we get
μ = tan θ
0.5 = x²/2
⇒ x² =1
⇒ x = ±1
Now, putting the value of x in y = x3/6, we get
When x =1

When x =-1

So, the maximum height above the ground at which the block can be placed without slipping is 1/6m.

When a rubber band is strecthed by a distance x, it exerts a restoring force of magnitude F = ax +bx², where a and b are constants. The work done in stretching are unstretched rubber-band by L is

• aL² +bL²

• 
• 
• 

C.

Given, F = ax +bx²
We know that work done in stretching the rubber band by L is 
|dW|= |Fdx|

A bob of mass m attached to an inextensible string of length l is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω rad/s about the vertical. About the point of suspension

• angular momentum is conserved

• angular momentum changes in magnitude but not in the direction

• angular momentum changes in direction but not in magnitude

• angular momentum changes both in direction and magnitude