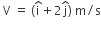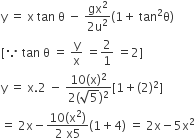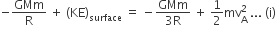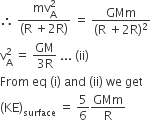A metallic rod of length ‘l’ is tied to a string of length 2l and made to rotate with angular speed ω on a horizontal table with one end of the string fixed. If there is a vertical magnetic field ‘B’ in the region, the e.m.f. induced across the ends of the rod is

• 
• 
• 
• 

D.

This question has Statement I and Statement II. Of the four choices given after the Statements, choose the
one that best describes the two Statements.
Statement – I: A point particle of mass m moving with speed v collides with stationary point particle of mass M. If the maximum energy loss possible is given as f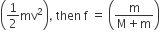 
Statement – II : Maximum energy loss occurs when the particles get stuck together as a result of the collision.

• Statement – I is true, Statement – II is true, Statement – II is a correct explanation of Statement – I.

• Statement – I is true, Statement – II is true, Statement – II is not a correct explanation of Statement – I.

• Statement – I is true, Statement – II is false.

• Statement – I is false, Statement – II is true 

Let [ε₀] denote the dimensional formula of the permittivity of vacuum. If M = mass, L = length, T = time and A = electric current, then

• [ε₀] = [M^-1L^-3T²A]

• [ε₀] = [M^-1L^-3T⁴A²]

• [ε₀] =[M^-2L²T^-1A^-2]

• [ε₀] = [M^-1L²T^-1A²]

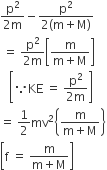
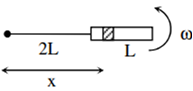
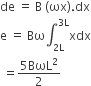
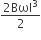
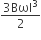
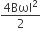
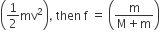
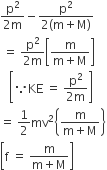
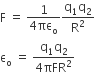
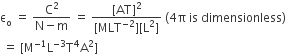
A projectile is given an initial velocity of  where is along the ground and  is along the vertical. If g = 10 m/s², the equation of its trajectory is: 

• y = x-5x2

• y = 2x-5x²

• 4y = 2x- 5x²

• 4y = 2x-25x²

What is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?

• 5GmM/6R

• 2GmM/3R

• GmM/2R

• GmM/3R